Triangulos

Un triangulo tiene tres ángulos y tres lados y la suma de sus tres ángulos interiores es 180º

Equilátero, isósceles y escaleno

Hay tres nombres especiales de triángulos que indican cuántos lados (o ángulos) son iguales.

Puede haber 3, 2 o ningún lados/ángulos iguales:

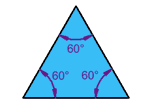	Triángulo equilátero Tres lados iguales Tres ángulos iguales, todos 60°
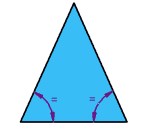	Triángulo isósceles Dos lados iguales Dos ángulos iguales
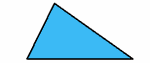	Triángulo escaleno No hay lados iguales No hay ángulos iguales

¿Qué tipos de ángulos?

Los triángulos también tienen nombres que te dicen los tipos de ángulos

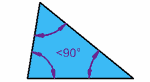	Triángulo acutángulo Todos los ángulos miden menos de 90°
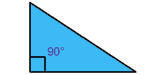	Triángulo rectángulo Tiene un ángulo recto (90°)
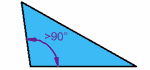	Triángulo obtusángulo Tiene un ángulo mayor que 90°

Combinar los nombres

A veces los triángulos tienen dos nombres, por ejemplo: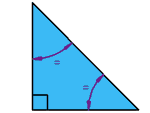

Triángulo isósceles rectángulo Tiene un ángulo recto (90°), y los otros dos ángulos iguales ¿Adivinas cuánto miden? Si, 45º

Área

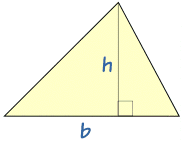Área = ½bh

La fórmula (1/2)bh vale para todos los triángulos. Asegúrate de que la "h" la mides perpendicularmente a la "b".

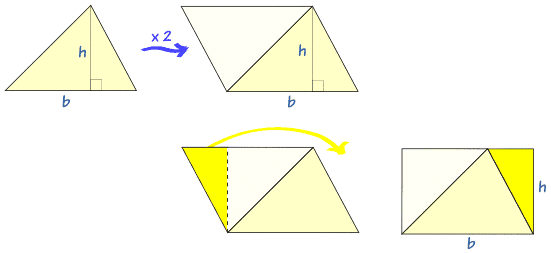
Imagina que "doblas" el triángulo (volteándolo a lo largo de uno de los lados de arriba) para tener una figura de cuatro lados (que será en realidad un "paralelogramo"), entonces el área sería bh. Pero eso son dos triángulos, así que uno solo es (1/2)bh.

Ternas pitagóricas

Son simplemente números enteros que cumplen la regla:

a² + b² = c²

(esta es la ecuación del teorema de Pitágoras)

Algunos ejemplos:

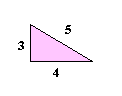Triángulo 3,4,5	Triángulo 5,12,13	Triángulo 9,40,41
32 + 42 = 52	52 + 122 = 132	92 + 402 = 412

Fuente: http://www.disfrutalasmatematicas.com/geometria/pitagoricas-ternas.html