Concepto de línea.
Todas las figuras, en último análisis, están
compuestas por puntos, que es la unidad gráfica mínima.
Una cierta cantidad de puntos situados cada uno
junto al otro, en una misma dirección, dan origen a un trazo contínuo, que es
una línea.
dirección, dan origen a un trazo contínuo, que es
una línea.
Una línea es una sucesión contínua de puntos:
——————————————
Las
líneas pueden ser:
- Rectas —
cuando todos los puntos se encuentran alineados en una misma dirección.
Curvas — cuando los puntos no se encuentran
alineados en una misma dirección; aunque, al menos durante cierta distancia, el
cambio de dirección responda a un criterio de continuidad.
La línea recta, la semirrecta, el segmento de recta.
Si bien una línea recta se dibuja siempre con
una cierta extensión delimitada — por razones prácticas dado que sería
imposible dibujar una recta sin final — en geometría se utiliza el concepto
ideal de que una recta es de longitud infinita en sus dos extremos.
A los efectos de su individualización en el
estudio, las líneas rectas se designan con una letra minúscula, siguiendo
el orden del abecedario:
a
b
Cuando se desea delimitar una recta, se marca
sobre ella un punto, al cual se llamaorigen. También por un motivo
convencional, en geometría todo punto se individualiza con una letra
mayúscula, siguiendo el orden alfabético.
Cuando en una recta se encuentra marcado un origen,
A, cada uno de los tramos a partir del origen, constituye una semirrecta:
a
A b
———————|—————
Cuando en una recta se marcan sobre ella dos puntos,
a los cuales se llamaextremos, el tramo de recta comprendido entre esos dos
puntos constituye unsegmento de recta; que se individualiza mencionando
sus extremos, como el segmento A,B:
A
B
——|———————|———
Generalmente, se traza un segmento solamente entre
sus extremos:
A
B
|—————|
Clases de líneas rectas en el espacio.
Atendiendo a la posición que una recta asume
en el espacio, en relación a la fuerza de gravedad o atracción terrestre
Clases de rectas en un plano.
Dos rectas — o más — pueden encontrarse entre
sí en distintas posiciones posibles:
|
|
|
· Dos rectas ubicadas en el mismo plano se
denominan paralelas — cuando todos los puntos de ambas se
encuentran a la misma distancia.
· Dos rectas ubicadas en el mismo plano se
denominan divergentes — cuando los puntos de ambas van aumentando
su distancia.
· Dos rectas ubicadas en el mismo plano se
denominan convergentes — cuando los puntos de ambas van dismuyendo
su distancia; y eventualmente ambas rectas se cruzan en un punto.
|
Es fácil advertir que en los dos últimos
casos, en realidad se está haciendo referencia a semirrectas; por cuanto las
divergentes resultan convergentes si se invierte el sentido de la comparación
de sus distancias, y las convergentes, luego de cruzarse, se tornan
divergentes.
|
|
|
Clases de rectas convergentes.
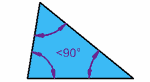
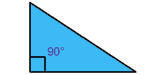
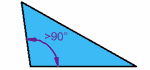
Las rectas convergentes, pueden ser:
- Perpendiculares — cuando dividen el
plano en cuatro partes iguales; es decir, cuando al cruzarse ninguna
resulta estar inclinada respecto de la otra.
·
Oblicuas — cuando se cruzan en
forma inclinada entre ellas, y por lo tanto dividen el plano en cuatro sectores
de los cuales dos son iguales, pero distintos de los otros dos que a su vez
son iguales entre sí.
|